Mathematical Optimization-Culled from http://en.wikipedia.org/wiki/Mathematical_optimization
In mathematics, statistics, empirical sciences, computer science, or managemect science, mathematical optimization (alternatively, optimization or mathematical programming) is the selection of a best element (with regard to some criteria) from some set of available alternatives.
In the simplest case, an optimization problem consists of maximizing or minimizing a real function by systematically choosing input values from within an allowed set and computing the value of the function. The generalization of optimization theory and techniques to other formulations comprises a large area of applied mathematics. More generally, optimization includes finding "best available" values of some objective function given a defined domain, including a variety of different types of objective functions and different types of domains.
Optimization problems
An optimization problem can be represented in the following way
-
Given: a function f : A
 R from some set A to the
real
numbers
R from some set A to the
real
numbers - Sought: an element x0 in A such that f(x0) ≤ f(x) for all x in A ("minimization") or such that f(x0) ≥ f(x) for all x in A ("maximization").
Such a formulation is called an optimization problem or a mathematical programming problem (a term not directly related to computer programming, but still in use for example in linear programming - see History below). Many real-world and theoretical problems may be modeled in this general framework. Problems formulated using this technique in the fields of physics and computer vision may refer to the technique as energy minimization, speaking of the value of the function f as representing the energy of the system being modeled.
Typically, A is some subset of the Euclidean space Rn, often specified by a set of constraints, equalities or inequalities that the members of A have to satisfy. The domain A of f is called the search space or the choice set, while the elements of A are called candidate solutions or feasible solutions.
The function f is called, variously, an objective function, cost function (minimization), utility function (maximization), or, in certain fields, energy function, or energy functional. A feasible solution that minimizes (or maximizes, if that is the goal) the objective function is called an optimal solution.
By convention, the standard form of an optimization problem is stated in terms of minimization. Generally, unless both the objective function and the feasible region are convex in a minimization problem, there may be several local minima, where a local minimum x* is defined as a point for which there exists some δ > 0 so that for all x such that
the expression
holds; that is to say, on some region around x* all of the function values are greater than or equal to the value at that point. Local maxima are defined similarly.
A large number of algorithms proposed for solving non-convex problems – including the majority of commercially available solvers – are not capable of making a distinction between local optimal solutions and rigorous optimal solutions, and will treat the former as actual solutions to the original problem. The branch of applied mathematics and numerical analysis that is concerned with the development of deterministic algorithms that are capable of guaranteeing convergence in finite time to the actual optimal solution of a non-convex problem is called global optimization.
Notation
Optimization problems are often expressed with special notation. Here are some examples.
Minimum and maximum value of a function
Consider the following notation:
This denotes the minimum
value of the objective function
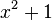 ,
when choosing x from the set of
real
numbers
,
when choosing x from the set of
real
numbers
 .
The minimum value in this case is
.
The minimum value in this case is
 ,
occurring at
,
occurring at
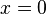 .
.
Similarly, the notation
asks for the maximum value of the objective function 2x, where x may be any real number. In this case, there is no such maximum as the objective function is unbounded, so the answer is "infinity" or "undefined".
Optimal input arguments
Consider the following notation:
or equivalently
This represents the value (or values) of the
argument x in the
interval
![(-\infty,-1]](http://upload.wikimedia.org/math/2/b/b/2bbda46f09c030f245f9afe1fa0eb85f.png) that minimizes (or minimize) the objective function x2 + 1
(the actual minimum value of that function is not what the problem asks for). In
this case, the answer is x = -1, since x = 0 is infeasible, i.e.
does not belong to the
feasible set.
that minimizes (or minimize) the objective function x2 + 1
(the actual minimum value of that function is not what the problem asks for). In
this case, the answer is x = -1, since x = 0 is infeasible, i.e.
does not belong to the
feasible set.
Similarly,
or equivalently
represents the
 pair (or pairs) that maximizes (or maximize) the value of the objective function
pair (or pairs) that maximizes (or maximize) the value of the objective function
 ,
with the added constraint that x lie in the interval
,
with the added constraint that x lie in the interval
![[-5,5]](http://upload.wikimedia.org/math/7/2/8/728629d5db271bc36f160c71b422fa90.png) (again, the actual maximum value of the expression does not matter). In this
case, the solutions are the pairs of the form (5, 2kπ) and (−5,(2k+1)π),
where k ranges over all integers.
(again, the actual maximum value of the expression does not matter). In this
case, the solutions are the pairs of the form (5, 2kπ) and (−5,(2k+1)π),
where k ranges over all integers.
Arg min and arg max are sometimes also written argmin and argmax, and stand for argument of the minimum and argument of the maximum.
History
Fermat and Lagrange found calculus-based formulas for identifying optima, while Newton and Gauss proposed iterative methods for moving towards an optimum. Historically, the first term for optimization was "linear programming", which was due to George B. Dantzig, although much of the theory had been introduced by Leonid Kantorovich in 1939. Dantzig published the Simplex algorithm in 1947, and John von Neumann developed the theory of duality in the same year.
The term programming in this context does not refer to computer programming. Rather, the term comes from the use of program by the United States military to refer to proposed training and logistics schedules, which were the problems Dantzig studied at that time.
Later important researchers in mathematical optimization include the following:


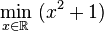

![\underset{x\in(-\infty,-1]}{\operatorname{arg\,min}} \; x^2 + 1,](http://upload.wikimedia.org/math/f/3/5/f356685bbb0bdac5fbffe93dc801f459.png)
![\underset{x}{\operatorname{arg\,min}} \; x^2 + 1, \; \text{subject to:} \; x\in(-\infty,-1].](http://upload.wikimedia.org/math/4/7/a/47a299410636b194b71cf02cc506df35.png)
![\underset{x\in[-5,5], \; y\in\mathbb R}{\operatorname{arg\,max}} \; x\cos(y),](http://upload.wikimedia.org/math/0/7/3/073cab0bbd77ec9324992a2f56467daa.png)
![\underset{x, \; y}{\operatorname{arg\,max}} \; x\cos(y), \; \text{subject to:} \; x\in[-5,5], \; y\in\mathbb R,](http://upload.wikimedia.org/math/2/a/1/2a1fae4789ea354904e7b3241eafc7ac.png)